Calibration of the Schöbel and Zhu (1999) Option Pricing Model

The class of exponential affine (jump) diffusions is a popular choice for the modeling of financial returns. One advantageous property of these models is their analytical tractability of the characteristic functions describing the returns distributions in Fourier space. A very well known model in this respect is the Heston (1993) stochastic volatility model, where the variance process is governed by a square-root process. Another approach is introduced by Schöbel and Zhu (1999); instead of the variance the volatility itself is modelled by an Ornstein–Uhlenbeck process.

Regarding the original formulation of the derived characteristic function, the model is usually not considered as an exponential affine model. With recent results from Gaspar (2004) and Cheng and Scaillet (2007) for quadratic models, Lord and Kahl (2006) provide a reformulated version of the Schöbel and Zhu (1999) characteristic function for which the space of state variables is augmented with an additional variance term. In this case, the characteristic function is exponentially affine in the state variables.

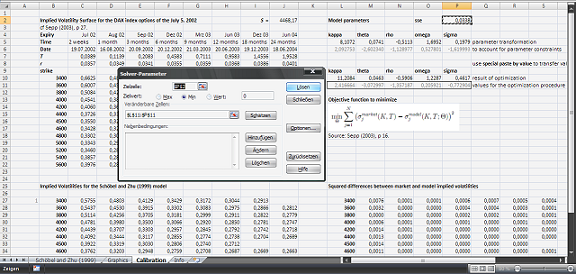
In this article the Schöbel and Zhu (1999) model is calibrated to a set of Black–Scholes implied volatilities as observed for DAX index options in a paper from Sepp (2003) about Fourier option pricing. Following the approach given by Sepp (2003), the MS Excel built-in Solver based on a Generalized Reduced Gradient (GRG) method is used for the optimization problem. To find a solution to the optimization problem the parameter vector is varied until the squared differences of the model implied volatilities to the market implied volatilities reach a minimum. This is known as the “method of least squares”. Generally, it must not be the case that a ‘global’ minimum is found in every case, as this kind of problems describes an ‘ill-posed’ problem. A successful calibration under this circumstances (i.e., without a global optimization) will depend on reasonably chosen initial values for the model parameter vector. Please note, that the implementation below is intended for illustration purposes only.

An optimization procedure via implied volatilities is computationally not the most efficient one, since in this case the resulting model option prices must be converted to implied volatilities by inverting a Black–Scholes pricing engine. This is especially true for an implementation in Excel – VBA.

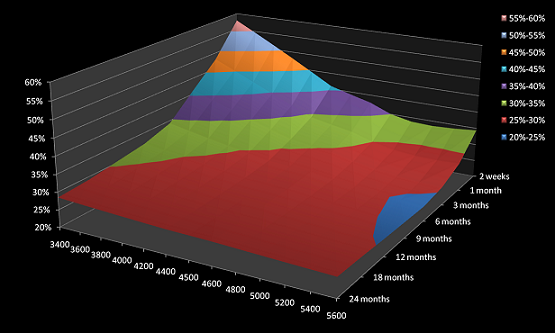
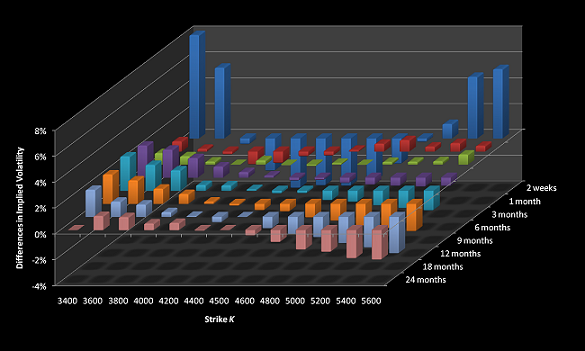
For a graphical demonstration see the example screenshots, more detailed information are contained in the download files below.

Calibration of the Schöbel and Zhu (1999) model with MS Excel’s Solver.

Calibration of the Schöbel and Zhu (1999) model with MS Excel’s Solver.

Model implied volatility surface of the Schöbel and Zhu (1999) option pricing model.

Model implied volatility surface.

Differences in implied volatility of the Schöbel and Zhu (1999) model and market values.

Differences in implied volatility.

References

  1. Cheng, Peng and Olivier Scaillet (2007) Linear-quadratic jump-diffusion modeling, Mathematical Finance 17(4), 575–598. DOI:10.1111/j.1467-9965.2007.00316.x
  2. Gaspar, Raquel M. (2004) General quadratic term structures of bond, futures and forward prices, SSE/EFI Working Paper Series in Economics and Finance, No. 559.
  3. Heston, Steven L. (1993) A closed-form solution for options with stochastic volatility with applications to bond and currency options, The Review of Financial Studies 6(2), 327–343. DOI:10.1093/rfs/6.2.327
  4. Lord, Roger and Christian Kahl (2006) Why the rotation count algorithm works, Discussion Paper TI 2006-065/2, Tinbergen Institute.
  5. Schöbel, Rainer and Jianwei Zhu (1999) Stochastic volatility with an Ornstein–Uhlenbeck process: An extension, European Finance Review 3(1), 23–46. DOI:10.1023/A:1009803506170
  6. Sepp, Artur (2003) Pricing European-style options under jump diffusion processes with stochastic volatility: Applications of Fourier transform, Working Paper, University of Tartu.

Download Files

Note: The Excel file(s) are developed with MS Excel 2007; for compatibility reasons I add a *.xls version for pre Excel 2007 versions (which are not tested). Both files are in a ‘zipped’ format.

Calibration of the Schöbel and Zhu (1999) Option Pricing Model (*.xlsm)

Calibration of the Schöbel and Zhu (1999) Option Pricing Model (*.xls)