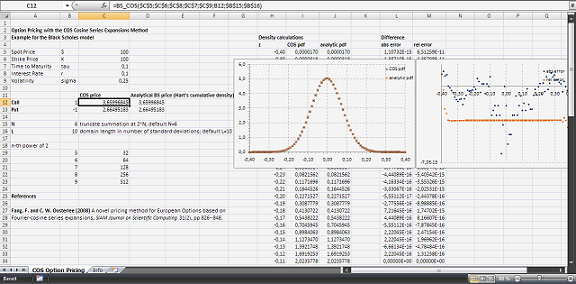
COS Fourier-Cosine Series Expansions and Option Pricing
Computationally efficient methods are required to price and calibrate complex financial models in reasonable time. A widely used technique for advanced price processes is based on Fourier inversion methods which in turn are usually implemented via numerical quadratures like FFT or direct integration algorithms. The valuation of derivatives instruments in image space offers a convenient way to sophisticated pricing problems, as long as the characteristic function for the price process is tractable either analytically or numerically.
Fang and Oosterlee (2008) propose an alternative approach, considering the close relation of the characteristic function with the series coefficients of the Fourier-cosine series expansion of the probability density function. This approach, which they christen the COS method, exhibits very competitive properties with respect to accuracy and computational efficiency.
This article shows how to recover the probability density and plain vanilla option prices with the COS method in a Black–Scholes world.
References
- Fang, Fang and Cornelis W. Oosterlee (2008) A novel pricing method for European options based on Fourier-cosine series expansions, SIAM Journal on Scientific Computing 31(2), 826–848. DOI:10.1137/080718061
Download Files
Note: The Excel file(s) are developed with MS Excel 2007; for compatibility reasons I add a *.xls version for pre Excel 2007 versions (which are not tested). Both files are in a ‘zipped’ format.
COS Fourier-Cosine Series Expansions and Option Pricing (*.xlsm)
COS Fourier-Cosine Series Expansions and Option Pricing (*.xls)