Complex Numbers in VBA
Mathematical operations on the complex plane have proven to facilitate many real world problems, or as Jacques Hadamard once remarked:
Jacques S. Hadamard (1865–1963)The shortest path between two truths in the real domain passes through the complex domain.
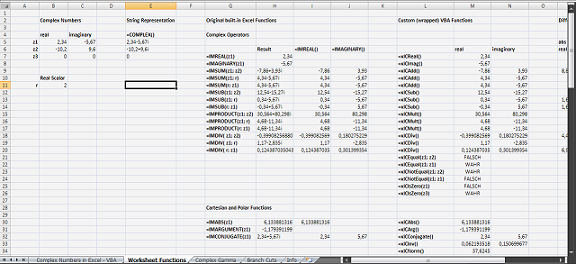
There are many mathematical packages, that handle complex numbers in a more or less native fashion. Excel, on the other hand, does not. Excel spreadsheets are a great tool for scientific and engineering computations, however the built-in support for complex numbers based on ‘string’ representations is computationally not very efficient and beside this fact only offers a basic set of elementary complex operations.
For this reason I wrote my own complex number library where the functions and operations pertaining to complex numbers are implemented by means of an User Defined Type (UDT):
Public Type Complex re As Double im As Double End Type
This library offers a comprehensive set of functions and is easily extendible. The functions implemented so far include:
Cartesian and Polar Functions
CNorm() Norm of Complex Number CAbs() Absolute Value of Complex Number; |z| CArg() Argument of Complex Number CConjugate() Conjugate of Complex Number CNeg() Negative of Complex Number; -z CSign() Signum function CInv() Complex inverse; 1 / z CHypotenuse() Length of the hypotenuse CRectangularToPolar() Convert Polar Coordiantes from Cartesian Complex CPolarToRectangular() Convert Cartesian Complex from Polar Coordinates
Exponential, Logarithms, Power and Root Functions
CExp() Complex Exponentiation CExp2() Exponent base 2 CExp10() Exponent base 10 CExpX() Exponent base X CLog() Log base e (Natural Log) of Complex Number CLog10() Log base 10 of Complex Number CLog2() Log base 2 of Complex Number CLogX() [Complex] Log base X of Complex Number CPow() Complex power with real exponent CPowC() Complex power with complex exponent CSquare() Second power CCubic() Third power CQuartic() Fourth power CSqrt() Square Root of Complex Number CRoot() [Complex] Root of Complex Number
Trigonometric and Hyperbolic Functions / Inverse Trigonometric and Inverse Hyperbolic Functions
CSin() Sine
CCos() Cosine
CTan() Tangent
CSec() Secant
CCoTan() Cotangent
CCoSec() Cosecant
CSinH() Hyperbolic Sine
CCosH() Hyperbolic Cosine
CTanH() Hyperbolic Tangent
CSecH() Hyperbolic Secant
CCoTanH() Hyperbolic Cotangent
CCoSecH() Hyperbolic Cosecant
CArcSin() Arc Sine
CArcCos() Arc Cosine
CArcTan() Arc Tangent
CArcCoTan() Arc Cotangent
CArcSec() Arc Secant
CArcCoSec() Arc Cosecant
CArcSinH() Hyperbolic Arc Sine
CArcCosH() Hyperbolic Arc Cosine
CArcTanH() Hyperbolic Arc Tangent
CArcCoTanH() Hyperbolic Arc Cotangent
CArcSecH() Hyperbolic Arc Secant
CArcCoSecH() Hyperbolic Arc Cosecant
CCis() Cis function; "cos + i sin"
Complex Operators
CAdd() Sum of two [Complex] Numbers CSub() Difference of two [Complex] Numbers CMult() Product of two [Complex] Numbers CDiv() Division of two [Complex] Numbers CEqual() Comparison operator CNotEqual() Comparison operator CIsZero() Test for zero real and imaginary part
Constants
I() Imaginary unit i MINUS_I() Negative imaginary unit -i ONE() Complex One MINUS_ONE() Complex minus One ZERO() Complex Zero
Special Functions
CGammaSpouge() Euler's Gamma function for complex arguments CGammaSpougeError() Relative error function for Gamma function using Spouge's formula CGammaSpougeLog() Complex Log Gamma function
As an additional benefit the majority of these functions are wrapped into functions that can be easily called
from within spreadsheets directly. To distinguish a VBA function from a worksheet function a ‘xl’ is used as a prefix.
For example CLog() then becomes xlCLog().
Further details and implementational issues are to be found in the download files.
Some example screenshots:
Complex Number Operations on a worksheet.
The Beauty of the Complex Gamma Function (imaginary part).
The Beauty of the Complex Log Gamma Function (abs).
Inverse Hyperbolic Sine Function (real part).
Complex Square Root Function (imaginary part).
Download Files
Note: The Excel file(s) are developed with MS Excel 2007; for compatibility reasons I add a *.xls version for pre Excel 2007 versions (which are not tested). Both files are in a ‘zipped’ format.
