Adaptive Quadrature in VBA
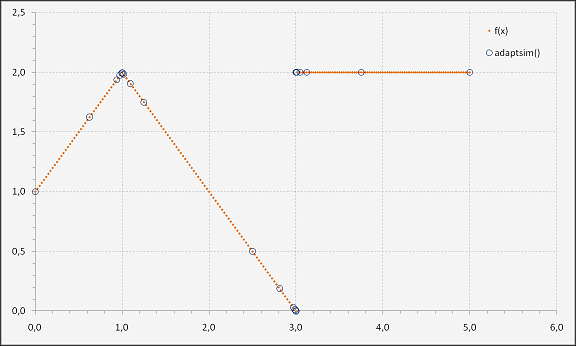
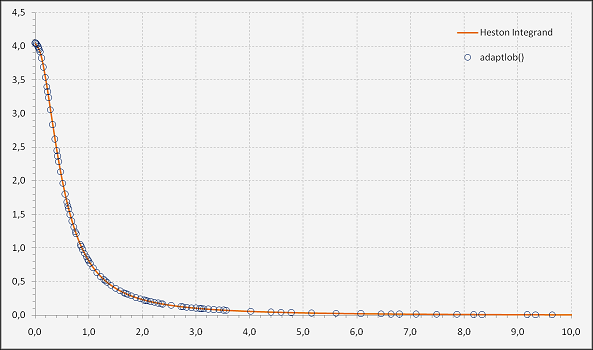
Adaptive algorithms are widely used for the numerical approximation of integrals. An adaptive quadrature is characterized by a procedure in which an interval of integration is recursively subdivided until a specific error tolerance is met. Gander and Gautschi (1998, 2000) published a paper describing two adaptive quadrature codes, adaptsim() and adaptlob(), which are proven to have good numerical characteristics in comparison to many other (including commercial) implementations. One is based on the Simpson’s quadrature rule and the other is a Lobatto formula with a Kronrod extension.
These two functions seem to be quite popular as they work really well; this article offers a translation to Excel – VBA. The implementation includes an experimental version of the Simpson’s rule, which accepts a function string as argument. However, for serious numerical work it is recommended to specify the integrand function as a proper VBA function.
For a graphical demonstration see the example screenshots, more detailed information are contained in the download files below.
Adaptive Simpson quadrature.
Adaptive Lobatto quadrature.
References
- Gander, Walter and Walter Gautschi (1998) Adaptive Quadrature—Revisited, Technical Report 306, ETH Zürich.
- Gander, Walter and Walter Gautschi (2000) Adaptive Quadrature—Revisited, BIT 40(1), 84–101. DOI:10.1023/A:1022318402393
Download Files
Note: The Excel file(s) are developed with MS Excel 2007; for compatibility reasons I add a *.xls version for pre Excel 2007 versions (which are not tested). Both files are in a ‘zipped’ format.
