Option Pricing with Tempered Stable Distributions
Numerous studies have shown that the assumptions of normally distributed returns underlying the Black–Scholes model (Black and Scholes, 1973; Merton, 1973) are not consistent with empirical stylized phenomena. For a lot of assets, their returns exhibit non-normal distributions with excess kurtosis and non-zero skewness. One family of distributions capable to explaining these stylized facts are the class of Lévy processes.
In particular, the class of “Tempered Stable Distributions” offers very promising properties with respect to the modeling of financial returns. Its parameters allow to control not only the location and the width of the distribution, but also the skewness and kurtosis of the distribution.
The tempered stable processes are studied under a number of different names, including the “CGMY” process (Carr et al., 2002), “KoBoL” process (Boyarchenko and Levendorskiĭ, 2000), and “Dampened Power Law” process (Wu, 2008). Depending on the parameter values the tempered stable process is able to resemble a infinite or finite activity stochastic process and might exhibit infinite or finite variation. Special cases include the Kou (2002) Double Exponential model, the Variance Gamma model from Madan et al. (1998) and an alpha stable process (see Wu, 2008).
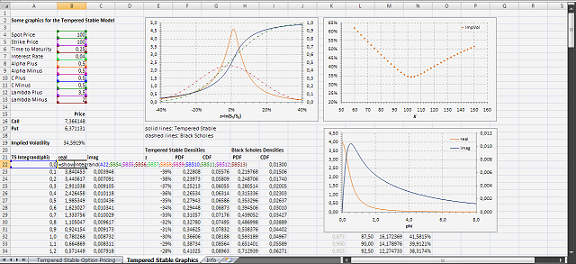
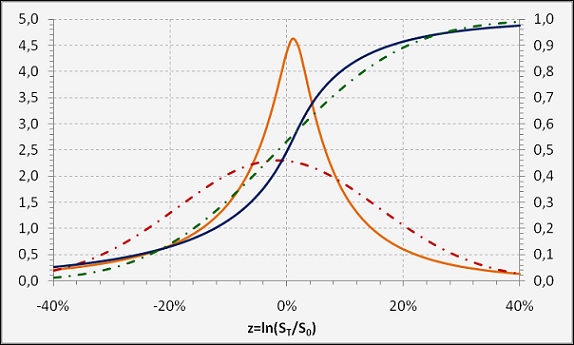
The illustration file implements the tempered stable process for plain vanilla options using the Fourier inversion method as developed in Lewis (2001) and Lipton (2002).
For a graphical demonstration see the example screenshots, more detailed information are contained in the download files below.
References
- Boyarchenko, Svetlana I. and Sergei Z. Levendorskiĭ (2002) Option pricing for truncated Lévy processes, International Journal of Theoretical and Applied Finance 3(3), 549–552. DOI:10.1142/S0219024900000541
- Carr, Peter, Hélyette Geman, Dilip B. Madan, and Marc Yor (2002) The fine structure of asset returns: An empirical investigation, The Journal of Business 75(2), 305–332.
- Kou, Steven G. (2002) A jump-diffusion model for option pricing, Management Science 48(8), 1086–1101. DOI:10.1287/mnsc.48.8.1086.166
- Lewis, Alan L. (2001) A simple option formula for general jump-diffusion and other exponential Lévy processes, Envision Financial Systems and OptionCity.net, California.
- Lipton, Alexander (2002) The vol smile problem, Risk, February, 61–65.
- Madan, Dilip B., Peter P. Carr and Eric C. Chang (1998) The variance gamma process and option pricing, European Finance Review 2(1), 79–105. DOI:10.1023/A:1009703431535
- Poirot, Jérémy and Peter Tankov (2006) Monte Carlo option pricing for tempered stable (CGMY) Processes, Asia-Pacific Financial Markets 13(4), 327–344. DOI:10.1007/s10690-007-9048-7
- Wu, Liuren (2008) Modeling financial security returns using Lévy processes, In: Handbooks in Operations Research and Management Science: Financial Engineering, Volume 15, Eds. J. R. Birge and V. Linetsky, Elsevier, North-Holland. DOI:10.1016/S0927-0507(07)15003-9
Download Files
Note: The Excel file(s) are developed with MS Excel 2007; for compatibility reasons I add a *.xls version for pre Excel 2007 versions (which are not tested). Both files are in a ‘zipped’ format.